6198. Minimum sum

There are two arrays of positive integers a_1..n and b_1..n. Find a permutation i₁, i₂, ..., i_n of numbers 1, 2, ..., n, for which the sum

a₁ * b_i1 + ... + a_n * b_in

is minimal. Each number should appear only once in the permutation.

Input. The first line contains the number of elements n (n ≤ 100) in the arrays. The second line contains the elements of the first array, and the third line contains the elements of the second array. The array elements do not exceed 10⁶.

Output. Print the minimal value of required sum.

Sample input	Sample output
5 7 2 4 3 10 5 11 6 9 6	165

SOLUTION

greedy

Algorithm analysis

Consider the case of arrays with two elements. Let A = {p, q} (p < q) and B = {x, y}. Let’s examine the condition under which the sum p * x + q * y will be minimized. Let’s consider two permutation options:

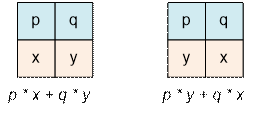
The inequality p * x + q * y < p * y + q * x holds if

x * (p – q) < y * (p – q)

Given that p ≠ q, dividing the inequality by (p – q) < 0, we obtain x > y. This means that the sum p * x + q * y (when p < q) will be minimized if x > y.

Consider a pair of elements from the original arrays A and B. If a_i < a_j and b_i < b_j, then by swapping b_i and b_j, we decrease the total sum.

Sort array a in ascending order and array b in descending order. Then we’ll obtain the sum with the smallest value

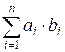
Example

Compute the sum for the given example.

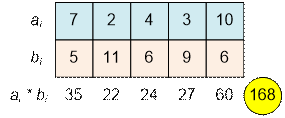
Let’s take a pair where a₁ < a₅ and b₁ < b₅. Swapping b₁ and b₅ will decrease the sum.

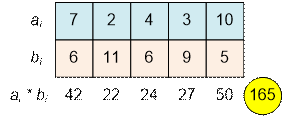
For the given example, for any pair (i, j), if a_i < a_j, then b_i > b_j. Therefore, the current permutation is optimal.

Let’s consider obtaining the minimum sum by sorting array a in ascending order and array b in descending order.

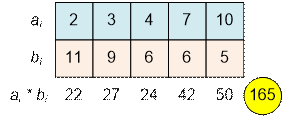
Algorithm realization

Declare the input arrays.

#define MAX 101

int a[MAX], b[MAX];

Read the input data.

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d",&a[i]);

for(i = 0; i < n; i++)

scanf("%d",&b[i]);

Sort the first array in ascending order, and the second array in descending order.

sort(a,a+n);

sort(b,b+n,greater<int>());

Compute the desired minimum sum, which can be a 64-bit integer.

res = 0;

for(i = 0; i < n; i++)

res += 1LL * a[i] * b[i];

Print the answer.

printf("%lld\n",res);

Algorithm realization – dynamic memory allocation

#include <cstdio>

#include <algorithm>

#include <set>

using namespace std;

int i, n;

int *a, *b;

long long res;

int main(void)

{

scanf("%d",&n);

a = new int[n];

for(i = 0; i < n; i++)

scanf("%d",&a[i]);

b = new int[n];

for(i = 0; i < n; i++)

scanf("%d",&b[i]);

sort(a,a+n);

sort(b,b+n,greater<int>());

for(res = i = 0; i < n; i++)

res += 1LL * a[i] * b[i];

printf("%lld\n",res);

delete[] a;

delete[] b;

return 0;

}

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

Integer a[] = new Integer[n];

for(int i = 0; i < n; i++)

a[i] = con.nextInt();

Integer b[] = new Integer[n];

for(int i = 0; i < n; i++)

b[i] = con.nextInt();

Arrays.sort(a);

Arrays.sort(b, Collections.reverseOrder());

long res = 0;

for(int i = 0; i < n; i++)

res += 1L * a[i] * b[i];

System.out.println(res);

con.close();

}

}

Python realization

Read the input data.

n = int(input())

l1 = list(map(int,input().split()))

l2 = list(map(int,input().split()))

Sort the first array in ascending order, and the second array in descending order.

l1.sort()

l2.sort(reverse = True)

Compute the desired minimum sum.

res = 0

for i in range(n):

res += l1[i] * l2[i]

Print the answer.

print(res)